by Peter Kuchnio
Download the Source
Introduction
In this tutorial we're going to be checking for collisions between irregularly shaped objects, or, any polygon we define around our image. We're going to be doing this the handy equation, y=mx+b to check for intersections (or collisions) between our lines. This method is more accurate then circle-based collision detection and is a better choice then pixel-perfect collision detection if you can define a polygon around your image that accurately reflects its boundaries. It has more limitations then pixel-perfect collision detection, but its also a lot faster =)
The Code
Data Structures
As the accuracy of our collision detection methods increases, so does the amount of data we need to store and process. So, before we begin we're going to have to create two custom types:
Private Type Vertex
x As Integer
y As Integer
End Type
'Defines the positions of the line segment
'and the rough area around it
Private Type LineSegment
Segment(0 To 1) As Vertex
LeftX As Integer
RightX As Integer
TopY As Integer
BottomY As Integer
End Type
|
|
The first data type is very simple, it simply lets us easily define the x and y coordinates of any point on the screen. The second type is a bit more complicated. First, it lets us define a line segment, or any two points on the screen which represent the endpoints of a line. To do this we use a 2 element array. The next part looks very similar to the RECT type, and it should. It lets us define the min and max coordinates around our line segment.
These two types are essential to checking for collisions between line segments. Now, we move on to declaring the rest of the variables and arrays that we'll need:
'Arrays to hold all of the vertex info for the two
'shapes we will be checking
Dim SegmentArray1() As LineSegment
Dim SegmentArray2() As LineSegment
'Variables to hold the positions of our ships
Dim Ship1X As Integer, Ship1Y As Integer
Dim Ship2X As Integer, Ship2Y As Integer
'Surfaces to hold image data
Dim Ship1 As DirectDrawSurface7
Dim Ship2 As DirectDrawSurface7
Dim Ship1RECT As RECT, Ship2RECT As RECT
'Api Declaration for IntersectRECT
Private Declare Function IntersectRect Lib "user32" (lpDestRect As RECT,
lpSrc1Rect As RECT, lpSrc2Rect As RECT) As Long
Dim running As Boolean
|
|
First, we define line segment arrays for both of our images. You'll need to declare one for every image that you want to check collisions between. Next we declare variables to hold the coordinates of our ships (the images we're using are space ships) and some DirectDraw variables for actually drawing our images..
Loading the Collision Information Data
Now that we have our variables and data structures declared, we need to fill them with data =) Basically, we define points around our image and this creates the shape where a collision will occur. Setting this up by hand is tedious, so the source code includes a collision setup program which lets you easily define the necessary points around your image.
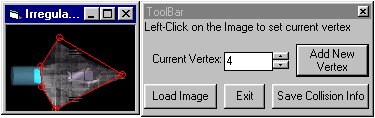
The data we need will be stored in text files, but it would be easily to modify the code to use binary files instead. Here is how we load our data into the program:
Private Sub LoadColData(FilePath As String, SegArray() As LineSegment)
''This subroutine loads the collision data from a specified file
''and fills out the line segment array
Dim CurrentLine As String
Dim VerticesInFile As Integer
Dim VArray() As Vertex
Dim I As Integer
Open FilePath For Input As #1
'How many vertices are we going to be loading
Line Input #1, CurrentLine
VerticesInFile = Val(Int(CurrentLine))
'Redimension array
ReDim VArray(0 To VerticesInFile)
'Load all of our vertices
For I = 0 To VerticesInFile
Line Input #1, CurrentLine
VArray(I).x = Val(Int(CurrentLine))
Line Input #1, CurrentLine
VArray(I).y = Val(Int(CurrentLine))
Next
Close #1
|
|
We create a function and pass it the path to the collision data file we are using and the Line Segment array that we want filled with data. The data file contains vertice information only, so we create a vertice array, go through the file, and load our coordinates into it. Now we have to fill out our line segment array and do some sorting work:
ReDim SegArray(0 To UBound(VArray))
Dim t As Integer
For t = 0 To UBound(VArray)
If t < UBound(VArray) Then
With SegArray(t)
.Segment(0).x = VArray(t).x
.Segment(0).y = VArray(t).y
.Segment(1).x = VArray(t + 1).x
.Segment(1).y = VArray(t + 1).y
'Check if the line we just got is vertical
'If it is we're going to use a bit of a dirty
'trick, and one point is going to be shifted
'over 1 pixel to the right.
If .Segment(0).x - .Segment(1).x = 0 Then
.Segment(0).x = .Segment(0).x + 1
End If
If .Segment(0).x <= .Segment(1).x Then
.LeftX = .Segment(0).x
.RightX = .Segment(1).x
Else
.LeftX = .Segment(1).x
.RightX = .Segment(0).x
End If
If .Segment(0).y <= .Segment(1).y Then
.TopY = .Segment(0).y
.BottomY = .Segment(1).y
Else
.TopY = .Segment(1).y
.BottomY = .Segment(0).y
End If
End With
|
|
We go thorugh our array, this part pertains to if we are not on the last element in the array. The next part deals with that. Basically we fill out the line segment array and we also put in a little trick. If the line is vertical, we shift one of x coordinates over 1 pixel to the right. This is so we don't have to deal with vertical lines, which would take a lot more code and processing in the collision detectoin function. We also define the min and max coordinates around the line segment (ie: a box or RECT).
If we are on the last point in our array, we wrap it around, so the last element connects to the first one. This makes a closed figure.
Else
'wrap it around so the last point makes
'a line segment with the first point.
With SegArray(t)
.Segment(0).x = VArray(t).x
.Segment(0).y = VArray(t).y
.Segment(1).x = VArray(0).x
.Segment(1).y = VArray(0).y
'Check if the line we just got is vertical
'If it is we're going to use a bit of a dirty
'trick, and one point is going to be shifted
'over 1 pixel to the right.
If .Segment(0).x - .Segment(1).x = 0 Then
.Segment(0).x = .Segment(0).x + 1
End If
If .Segment(0).x <= .Segment(1).x Then
.LeftX = .Segment(0).x
.RightX = .Segment(1).x
Else
.LeftX = .Segment(1).x
.RightX = .Segment(0).x
End If
If .Segment(0).y <= .Segment(1).y Then
.TopY = .Segment(0).y
.BottomY = .Segment(1).y
Else
.TopY = .Segment(1).y
.BottomY = .Segment(0).y
End If
End With
End If
Next
End Sub
|
|
That's it for the loading subroutine =)
Checking for Collisions
This is the hard part =) We now have to create a function that checks for collisions, or intersections between all of the line segments we have defined. Before we get down to the math however, we will again have to work a bit with the data we have:
Private Function CheckIrregularCollision(X1 As Integer, Y1 As Integer,
SegArray1() As LineSegment, X2 As Integer, Y2 As Integer,
SegArray2() As LineSegment) As Boolean
'Checks for collisions between irregularly shaped objects
'(ie: polygons). We pass it the x and y coordinates of the image
'we are drawing and the collision arrays that have previously
'been set-up that define the points around the image.
'Arrays between which we will be checking collisions
Dim Collision1() As LineSegment
Dim Collision2() As LineSegment
'Redimension our collision arrays
ReDim Collision1(0 To UBound(SegArray1))
ReDim Collision2(0 To UBound(SegArray2))
'Fill the collision arrays we just set up with the varrays
'we passed the function
'We also translate our vertices to where they appear on the screen
Dim A As Integer, I As Integer
For I = 0 To UBound(Collision1)
With Collision1(I)
.Segment(0).x = SegArray1(I).Segment(0).x + X1
.Segment(0).y = SegArray1(I).Segment(0).y + Y1
.Segment(1).x = SegArray1(I).Segment(1).x + X1
.Segment(1).y = SegArray1(I).Segment(1).y + Y1
.LeftX = SegArray1(I).LeftX + X1
.RightX = SegArray1(I).RightX + X1
.TopY = SegArray1(I).TopY + Y1
.BottomY = SegArray1(I).BottomY + Y1
End With
Next
For I = 0 To UBound(Collision2)
With Collision2(I)
.Segment(0).x = SegArray2(I).Segment(0).x + X2
.Segment(0).y = SegArray2(I).Segment(0).y + Y2
.Segment(1).x = SegArray2(I).Segment(1).x + X2
.Segment(1).y = SegArray2(I).Segment(1).y + Y2
.LeftX = SegArray2(I).LeftX + X2
.RightX = SegArray2(I).RightX + X2
.TopY = SegArray2(I).TopY + Y2
.BottomY = SegArray2(I).BottomY + Y2
End With
Next
|
|
We pass the x and y coordinates of the two objects we will be checking collisions between to the function as well as their line segment arrays. We now create two more arrays to hold their data, as we will be modifying these arrays and we don't want these changes actually changed in the real arrays we have loaded. What we have to do before we begin our maths is to translate all of the coordinates in the arrays to screen coordinates, so we add the x and y values we passed to the function to all of them.
Now, we have to declare some variables:
'Point at which an intersection is occuring
Dim IntersectX As Single, IntersectY As Single
'Slopes of our lines
Dim m1 As Single, m2 As Single
'Y-Intercepts for our lines
Dim b1 As Single, b2 As Single
'We only scan if our two line segments are intersecting if
'they are in proximity to each other. We check this using
'IntersectRECT.
Dim TempRECT1 As RECT
Dim TempRECT2 As RECT
Dim emptyrect As RECT
Dim TempResult1 As Integer
Dim TempResult2 As Integer
|
|
If you've been wondering what formula is used in the sample, this should answer it. We'll be using y=mx+b to find the point of intersectin between any two lines. The math is relativaly simple, we'll use substitution to find the point of intersection between two lines. So, we declare variables to hold the point of intersection and the slopes and y-intercepts of our lines.
However, checking the point of intersection for all lines every single cycle would be a lot of unnecessary processing, especially since we are dealing with line segments, not lines. This is where the LeftX, RightX, TopY and BottomY variables come into play. We'll be using the IntersectRECT API call to see if the two line segments we are currently checking are in proximity to each other. If they are, only then do we find their point of intersection and see if that point is on both lines.
So, we will have to create a nested loop, and check each of object 1's line segments against each of object 2's line segments. This example uses 5 line segments to define the area around our object, which makes for 25 cycles. You can see how inefficient this would get if we didn't check for line segment proximity before calculating the point of intersection.
For A = 0 To UBound(Collision1)
For I = 0 To UBound(Collision2)
'Only check if the two line segments we are checking are close
'enough together for a collision to occur
With TempRECT1
.Left = Collision1(A).LeftX - 1
.Right = Collision1(A).RightX + 1
.Top = Collision1(A).TopY - 1
.Bottom = Collision1(A).BottomY + 1
End With
With TempRECT2
.Left = Collision2(I).LeftX - 1
.Right = Collision2(I).RightX + 1
.Top = Collision2(I).TopY - 1
.Bottom = Collision2(I).BottomY + 1
End With
If IntersectRect(emptyrect, TempRECT1, TempRECT2) <> 0 Then
|
|
So, we start our loop, fill out RECT variables for the area around the line segment, and if we find any that are intersecting we move on to finding the point of intersection:
'get slope
m1 = ((Collision1(A).Segment(0).y - Collision1(A).Segment(1).y) /
(Collision1(A).Segment(0).x - Collision1(A).Segment(1).x))
m2 = ((Collision2(I).Segment(0).y - Collision2(I).Segment(1).y) /
(Collision2(I).Segment(0).x - Collision2(I).Segment(1).x))
|
|
First, we get the slopes for both of our line segments. This is done using deltaY / deltaX. Next, we have to calculate the y-intercepts for our lines:
'get y intercept
b1 = Collision1(A).Segment(0).y - (m1 * Collision1(A).Segment(0).x)
b2 = Collision2(I).Segment(0).y - (m2 * Collision2(I).Segment(0).x)
|
|
Finding the y-intercept for the line is done using the formula, b = y - (mx). Now that we have all the necessary information we can move on to finding the point at which the two lines intersect:
'Find the point of intersection
IntersectX = (b2 + (-(b1))) / (m1 + (-(m2)))
IntersectY = m1 * IntersectX + b1
'Draw a circle where the point of intersection is occuring
DDDrawCircle ddsBack, (IntersectX), (IntersectY), 1, RGB(0, 255, 0)
|
|
We find IntersectX by using substitution, so we sub one equation into the other, eliminating one variable. On paper this would look like : m1 * x1 + b1 = m2 * x2 + b2.
Once we have IntersectX, its easy to find IntersectY. We just sub the x value into the equation y=mx+b and get a result. We also draw a circle at the point where the interseection occured, this is just for feedback purposes, of course =)
The next part is checking if the point of intersection is actually on the two lines we are currently checking. This is done by using the formula, b=y-mx :
'Now, we check if the point of intersection is on both
'line segments. To do this we calculate the value for b
'given the point of intersection we found. We use the formula
'b=y-mx. If the result equals the y-intercept for both of our
'equations then we have a collision =)
TempResult1 = IntersectY - (m1 * IntersectX)
TempResult2 = IntersectY - (m2 * IntersectX)
If IntersectX >= Collision1(A).LeftX And IntersectX <=
Collision1(A).RightX Then
If IntersectY >= Collision1(A).TopY And IntersectY <=
Collision1(A).BottomY Then
If IntersectX >= Collision2(I).LeftX And IntersectX <=
Collision2(I).RightX Then
If IntersectY >= Collision2(I).TopY And IntersectY <=
Collision2(I).BottomY Then
If CInt(b1) = TempResult1 And CInt(b2) = TempResult2 Then
'Draw a circle where the collision has occured
DDDrawCircle ddsBack, (IntersectX), (IntersectY), 1,
RGB(0, 0, 255)
'Return that a collision has occured
CheckIrregularCollision = True
'Exit the function
Exit Function
End If
End If
End If
End If
End If
End If
Next
Next
End Function
|
|
We sub IntersectX and IntersectY into our formula and store the result. Next, we check if the point of intersection is within the area of the line segment. If it is we check if the y-intercepts calculated before equal the y-intercepts that we just calculated using IntersectX and IntersectY. If they do, that means that the two lines are intersecting and we have a collision! =) The result is rounded so that even if the numbers are .001 off we still get a collison.
Well, that's it!. Once you pass the right coordinates and arrays to this function it will return wether a collision is occuring.
Applying the Functions
Now that the functions have been created, its very easy to use them in a sample. First, we load our collision data in the Form_Load subroutine:
Private Sub Form_Load()
'Initialize Directdraw
ddInit Form1, 800, 600, 16
'Load our graphics
DDCreateSurface Ship1, App.Path & "\circlecol1.bmp", Ship1RECT
DDCreateSurface Ship2, App.Path & "\circlecol2.bmp", Ship2RECT
'Initial positions of our ships
Ship1X = 50
Ship1Y = 50
Ship2X = 600
Ship2Y = 400
'Load vertices which define the area we will be checking collisions
'between
LoadColData App.Path & "\irregularcol1.txt", SegmentArray1
LoadColData App.Path & "\irregularcol2.txt", SegmentArray2
'show the form
Me.Show
running = True
Main_Loop
End Sub
|
|
This sub also initializes DirectDraw and loads our images, as well as setting up some initial values. After everything has been loaded and initialized we call the subroutine Main_Loop, where we will scan for collisions.
Private Sub Main_Loop()
''Our main loop that will take care of drawing and collision
''detection
Do
DoEvents
'Fill the screen with black
DDColorFill ddsBack, 0, 0, 800, 600, RGB(0, 0, 0)
'write instructions
ddsBack.DrawText 0, 0, "Use the arrow keys to move the ship", False
'Draw the ships
DDBltFast Ship1, Ship1RECT, Ship1X, Ship1Y
DDBltFast Ship2, Ship2RECT, Ship2X, Ship2Y
'Check for collisions
If CheckIrregularCollision(Ship1X, Ship1Y, SegmentArray1, Ship2X,
Ship2Y, SegmentArray2) = True Then
'If a collision has occured we write something to the
'screen. In a real game you'd probably do something
'more useful with this information =)
ddsBack.DrawText 0, 20, "Collision!", False
End If
DDFlip
Loop Until running = False
End Sub
|
|
This is all very simple, we draw our ships and the last part checks if a collision has occured. We simply pass the x and y coordinates of the two ships we are checking between and their line segment arrays.
Conclusion
Well, that's it! We can now easily check for collisons between any shaped polygons we define around our sprites. This is a very accurate form of collision detection, since you don't have to generalize the shape of your image into a circle or rectange. Make sure to download the source to see the example in action.
|
